Problemstellung: Es geht eine Trajektorie von irgend einem Startpunkt zu irgend einem Zielpunkt.
Es sollen die Strecken berechnet werden, die die Trajektorie durch die Boxen eines geographischen
Gitters (z.B. 2x2 Grad) läuft.
Sinn: Der Wind weht entlang der Trajektorie und sammelt aus jeder Gitterbox je nach Untergrund
(Wasser, Land mit Bewuchs vom Typ X) entsprechend der in der Box zurück gelegten Strecke Pollen auf.
Annahmen:
Bezeichnungen: Zur Berechnung des sphärischen Dreiecks werden die geographischen Breiten umgerechnet,
so dass ![]() ist. Die im folgenden verwendeten Koordinaten
ist. Die im folgenden verwendeten Koordinaten ![]() geben
also die Entfernung vom Nordpol an (siehe Abb. 1).
Die Trajektorie beginnt bei einem Punkt A (Koordinaten: Länge
geben
also die Entfernung vom Nordpol an (siehe Abb. 1).
Die Trajektorie beginnt bei einem Punkt A (Koordinaten: Länge ![]() und
Breite
und
Breite ![]() ) und endet bei Punkt B
(
) und endet bei Punkt B
(![]() ). Die Strecke der Trajektorie
von A nach B sei S. Der Winkel zwischen dem
). Die Strecke der Trajektorie
von A nach B sei S. Der Winkel zwischen dem ![]() und der Trajektorie sei
und der Trajektorie sei ![]() ,und der am Nordpol
,und der am Nordpol ![]() . Wenn A und B in einer gemeinsamen
Gitterbox liegen, reichen die Koordinaten von A und B zur Berechnung von S. Wenn B in einer anderen
Box als A liegt, so muss die Trajektorie die Box von A verlassen und es ist das Stück
. Wenn A und B in einer gemeinsamen
Gitterbox liegen, reichen die Koordinaten von A und B zur Berechnung von S. Wenn B in einer anderen
Box als A liegt, so muss die Trajektorie die Box von A verlassen und es ist das Stück ![]() der
Trajektorie zu berechnen, das in der Box von A liegt. Der Punkt an dem die Trajektorie die Box von A
verläßt sei der Kreuzungspunkt K
der
Trajektorie zu berechnen, das in der Box von A liegt. Der Punkt an dem die Trajektorie die Box von A
verläßt sei der Kreuzungspunkt K ![]() .
Dabei kann die Trajektorie entweder durch eine von einem Längengrad
oder eine von einem Breitengrad gebildete Boxgrenze gehen. (Natürlich auch genau durch beide, also eine
Box-Ecke. Das ist aber egal, weil dann die Berechnung für beide Typen zum Ziel führt.)
.
Dabei kann die Trajektorie entweder durch eine von einem Längengrad
oder eine von einem Breitengrad gebildete Boxgrenze gehen. (Natürlich auch genau durch beide, also eine
Box-Ecke. Das ist aber egal, weil dann die Berechnung für beide Typen zum Ziel führt.)
Die Grenzen der Box seien durch ![]() ,
, ![]() ,
, ![]() und
und ![]() gegeben.
Wenn S die Box durch eine Breitengradgrenze verlässt, so ist die Breite dieses Schnittpunktes
gegeben.
Wenn S die Box durch eine Breitengradgrenze verlässt, so ist die Breite dieses Schnittpunktes
![]() oder
oder ![]() . Der Längengrad des Schnittpunktes wird mit
. Der Längengrad des Schnittpunktes wird mit
![]() bezeichnet. Entsprechend ist
bezeichnet. Entsprechend ist ![]() der Breitengrad des Schnittpunktes K
beim Verlassen der Box durch einen Längengrad (0 oder 1).
der Breitengrad des Schnittpunktes K
beim Verlassen der Box durch einen Längengrad (0 oder 1).
Gleichungen zur Berechnung der benötigten Größen:
(Beachte: ![]() ist nicht die geographische Breite selbst sondern 90 - geogr. Breite !)
ist nicht die geographische Breite selbst sondern 90 - geogr. Breite !)
1.) Länge der geodätischen Linie S von 2 Punkten A (![]() ) und B (
) und B (![]() ):
):
Betrachtet wird das Dreieck (A, B, Nordpol).
Dann erhält man S (Strecke A - B) aus dem Seiten-Kosinussatz:
| |
(1) |
2.) Berechnung des Winkel ![]() zwischen S (von A nach B) und dem
Längengrad von A (
zwischen S (von A nach B) und dem
Längengrad von A (![]() ):
):
Betrachtet wird das Dreieck (A, B, Nordpol). Mit Kenntnis von S aus (1) erhält man den
Winkel ![]() aus dem Sinussatz:
aus dem Sinussatz:
| |
(2) |
3.) Berechnung von ![]() des Schnittpunktes K
(
des Schnittpunktes K
(![]() ) der Trajektorie mit der
Boxkante
) der Trajektorie mit der
Boxkante ![]() beim Verlassen der Box durch einen Längengrad:
beim Verlassen der Box durch einen Längengrad:
Betrachtet wird das Dreieck (A, K, Nordpol). Der Kotangenssatz läßt sich hierfür schreiben als
| |
(3) |
und Auflösen nach ![]() liefert:
liefert:
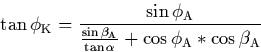 |
(4) |
4.) Berechnung von ![]() des Schnittpunktes K
(
des Schnittpunktes K
(![]() ) der Trajektorie mit der
Boxkante
) der Trajektorie mit der
Boxkante ![]() beim Verlassen der Box durch einen Breitengrad:
beim Verlassen der Box durch einen Breitengrad:
Betrachtet wird das Dreieck (A, K, Nordpol).
Zunächst wird mit dem Sinussatz der Winkel ![]() zwischen der Trajektorie S
und dem gesuchten Längengrad
zwischen der Trajektorie S
und dem gesuchten Längengrad ![]() bestimmt:
bestimmt:
| |
(5) |
Mit Hilfe der Neperschen Analogie kann der Winkel ![]() bestimmt werden:
bestimmt werden:
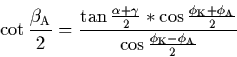 |
(6) |
und
| |
(7) |
Die obigen Gleichungen gelten für sphärische Dreiecke wie in Abb. 1.
Für Berechnungen tatsächlicher Trajektorien, die von und in alle möglichen Richtungen
weisen müssen aber viele verschiedene Fälle unterschieden werden,
z.B. ![]() und
und ![]() . Eine weitere
Komplikation besteht darin, dass eine Trajektorie einen Längengrad zwar nicht zwei mal schneiden kann
(solange sie kleiner als
. Eine weitere
Komplikation besteht darin, dass eine Trajektorie einen Längengrad zwar nicht zwei mal schneiden kann
(solange sie kleiner als ![]() sind),
weil sowohl Trajektorie als auch Längengrad Großkreise sind. Für Breitenkreise stimmt dies
aber nicht. Wenn der Startpunkt A genau auf dem Breitenkreis eines Boxrandes liegt (und das ist
bei der Berechnung von Boxgrenze zu Boxgrenze ziemlich häufig), dann kann man aus
sind),
weil sowohl Trajektorie als auch Längengrad Großkreise sind. Für Breitenkreise stimmt dies
aber nicht. Wenn der Startpunkt A genau auf dem Breitenkreis eines Boxrandes liegt (und das ist
bei der Berechnung von Boxgrenze zu Boxgrenze ziemlich häufig), dann kann man aus
![]() nicht folgern, dass die in Trajektorienrichtung nächste Box
auch
nicht folgern, dass die in Trajektorienrichtung nächste Box
auch ![]() hat. Der Großkreis kann zunächst in die geographisch andere
Richtung gehen. Um die nächste zu betrachtende Box zu erhalten wird in diesem Fall (Punkt A
auf Breitenkreis eines Boxrandes) die lokale Ableitung der Länge der Trajektorie S nach
hat. Der Großkreis kann zunächst in die geographisch andere
Richtung gehen. Um die nächste zu betrachtende Box zu erhalten wird in diesem Fall (Punkt A
auf Breitenkreis eines Boxrandes) die lokale Ableitung der Länge der Trajektorie S nach
![]() gebildet. Dann gilt
gebildet. Dann gilt
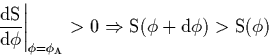 |
(8) |
und die nächste Box in Richtung Punkt B hat die 2. Boxkante mit ![]() .
Wenn man also in (1)
.
Wenn man also in (1) ![]() durch
durch ![]() ersetzt und die
Ableitung bildet erhält man
ersetzt und die
Ableitung bildet erhält man
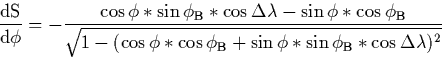 |
(9) |
Aus dem Wert von ![]() läßt sich also entscheiden, in welche Richtung
die Trajektorie läuft.
läßt sich also entscheiden, in welche Richtung
die Trajektorie läuft.
Literatur:
Bartsch: Mathematische Formeln. 1986. Buch- und Zeit-Verlagsgesellschaft mbH, Köln.
ISBN 3-8166-9060-2
Bigalke: Kugelgeometrie. 1984. Otto Salle Verlag GmbH, Frankfurt/Main.
ISBN 3-7935-5530-5
Sigl: Ebene und sphärische Trigonometrie mit Anwendungen auf Kartographie, Geodäsie und
Astronomie. 1977. Herbert Wichmann Verlag GmbH, Karlsruhe.
ISBN 3-87907-050-4
Bronstein, Semendjajew: Taschenbuch der Mathematik. 1976. Verlag Harri Deutsch, Zürich,...
ISBN 3-87144-016-7
Ja, ich weiß auch dass man nicht so viele Bücher für die paar Gleichungen braucht. Ich fand sie aber alle auf ihre Art hilfreich und so ist die Liste eher für mich falls ich mal wieder ein Buch zum rumkugeln suche.